import kwant
import matplotlib
import matplotlib.pyplot as plt
import scipy as scp
import numpy as np
from kwant.physics import dispersion
from scipy import sparse as sp
def make_system(a=1, t_1=1.0, t_2=1.0, L=10, lead=True):
lat = kwant.lattice.Polyatomic(
[[2 * a, 0], [0, 2 * a]], [[0, 0], [0, a], [a, 0]], norbs=1
)
lat.a, lat.b, lat.c = lat.sublattices
syst = kwant.Builder()
# Onsites
syst[(lat.a(n, m) for n in range(L) for m in range(L))] = 0
syst[(lat.b(n, m) for n in range(L) for m in range(L))] = 0
syst[(lat.c(n, m) for n in range(L) for m in range(L))] = 0
# Hopping t1
syst[((lat.a(n, m), lat.b(n, m)) for n in range(L) for m in range(L))] = t_1
syst[((lat.a(n, m), lat.c(n, m)) for n in range(L) for m in range(L))] = t_1
syst[((lat.b(n, m), lat.c(n, m)) for n in range(L) for m in range(L))] = t_2
syst[((lat.b(n + 1, m), lat.c(n, m)) for n in range(L - 1) for m in range(L))] = t_2
syst[((lat.b(n, m - 1), lat.c(n, m)) for n in range(L) for m in range(1, L))] = t_2
syst[
((lat.b(n - 1, m + 1), lat.c(n, m)) for n in range(1, L) for m in range(L - 1))
] = t_2
syst[((lat.b(n, m), lat.a(n, m + 1)) for n in range(L) for m in range(L - 1))] = t_1
syst[((lat.c(n, m), lat.a(n + 1, m)) for n in range(L - 1) for m in range(L))] = t_1
# Hopping t2
if lead == False:
return syst, lat
# Left lead
sym_left_lead = kwant.TranslationalSymmetry([-2 * a, 0])
left_lead = kwant.Builder(sym_left_lead)
# Onsites
left_lead[(lat.a(n, m) for n in range(L) for m in range(L))] = 0
left_lead[(lat.b(n, m) for n in range(L) for m in range(L))] = 0
left_lead[(lat.c(n, m) for n in range(L) for m in range(L))] = 0
# Hopping t1
left_lead[((lat.a(n, m), lat.b(n, m)) for n in range(L) for m in range(L))] = t_1
left_lead[((lat.a(n, m), lat.c(n, m)) for n in range(L) for m in range(L))] = t_1
left_lead[((lat.b(n, m), lat.c(n, m)) for n in range(L) for m in range(L))] = t_2
left_lead[
((lat.b(n + 1, m), lat.c(n, m)) for n in range(L - 1) for m in range(L))
] = t_2
left_lead[
((lat.b(n, m - 1), lat.c(n, m)) for n in range(L) for m in range(1, L))
] = t_2
left_lead[
((lat.b(n - 1, m + 1), lat.c(n, m)) for n in range(1, L) for m in range(L - 1))
] = t_2
left_lead[
((lat.b(n, m), lat.a(n, m + 1)) for n in range(L) for m in range(L - 1))
] = t_1
left_lead[
((lat.c(n, m), lat.a(n + 1, m)) for n in range(L - 1) for m in range(L))
] = t_1
syst.attach_lead(left_lead)
left_lead_fin = left_lead.finalized()
syst.attach_lead(left_lead.reversed())
syst_fin = syst.finalized()
return syst_fin, left_lead_fin, lat
def plot_bandstructure(flead, momenta, label=None, title=None):
bands = kwant.physics.Bands(flead)
energies = [bands(k) for k in momenta]
plt.figure()
plt.title(title)
plt.plot(momenta, energies, label=label)
plt.xlabel("momentum [(lattice constant)^-1]")
plt.ylabel("energy [t]")
def plot_conductance(syst, energies):
data = []
for energy in energies:
smatrix = kwant.smatrix(syst, energy)
data.append(smatrix.transmission(1, 0))
plt.figure()
plt.plot(energies, data)
plt.xlabel("energy [t]")
plt.ylabel("conductance [e^2/h]")
plt.show()
def plot_density(sys, ener, it=-1, title="empty"):
wf = kwant.wave_function(sys, energy=ener)
t = np.shape(wf(0))
nwf = wf(0)[0] * 0
for i in range(t[0] // 2 + 1):
test = wf(0)[i]
nwf += test
psi = abs(nwf) ** 2
if it == -1:
title = "density"
elif it > -1:
title = "density"
title2 = title + ".pdf"
kwant.plotter.map(sys, psi, method="linear", vmin=0, title=title)
J_0 = kwant.operator.Current(sys)
c = J_0(nwf)
kwant.plotter.current(sys, c)
plt.close()The Lieb lattice is a two dimensional square lattce with five atomic sites per unit cell.
The bases Hamiltonian with tight-binding approximation reads, \[H=t\sum_{\langle i,j \rangle}a^{\dagger}_{i}a_{j}+\tau \sum_{\langle\langle i,j \rangle\rangle}e^{i\phi_{ij}}a^{\dagger}_{i}a_{j},\] where hoppings \(t,\tau\in\mathbb{R}\) and the hopping between next-neighbour (NNN) is gifted with phase factor \(e^{i\phi_{ij}}\) where in order to keep Hamiltonian hermitian we need to have \(\phi_{ij}=\phi_{ji}\). To simplify we put \(\phi_{ij}=\phi\). Lattice vectors between nearest-neighbour (NN) are given by,
\[ \vec{a}_1=a \begin{pmatrix} 1 \cr 0 \end{pmatrix},\hspace{1cm} \vec{a}_2=a\begin{pmatrix} 0 \cr 1 \end{pmatrix} \], where \(a\) is a lattice constant.
In this model we distinguish three “kinds” of atoms: A atom in the center of cell, B translated by \(\vec{a}_{1}\) relaivly to A and atom C translated by vector \(\vec{a}_{2}\) relativly to atom A. Then the exact form of NN Hamiltonian, \[H_{NN}=t\sum_{i}\left(a^{\dagger}_{\vec{R}_{i}}b_{\vec{R}_{i}+\vec{a}_{1}}+a^{\dagger}_{\vec{R}_{i}}b_{\vec{R}_{i}-\vec{a}_{1}}+a^{\dagger}_{\vec{R}_{i}}c_{\vec{R}_{i}+\vec{a}_{2}}+a^{\dagger}_{\vec{R}_{i}}c_{\vec{R}_{i}-\vec{a}_{2}}\right)+h.c.\] and NNN Hamiltonian, \[ H_{NNN}=\tau e^{i\phi}\sum_{i}\left(b^{\dagger}_{\vec{R}_{i}+\vec{a}_{1}}c_{\vec{R}_{i}+\vec{a}_{2}}+c^{\dagger}_{\vec{R}_{i}-\vec{a}_{2}}b_{\vec{R}_{i}+\vec{a}_{1}}+b^{\dagger}_{\vec{R}_{i}-\vec{a}_{1}}c_{\vec{R}_{i}-\vec{a}_{2}}+c^{\dagger}_{\vec{R}_{i}+\vec{a}_{2}}b_{\vec{R}_{i}-\vec{a}_{1}}\right)+h.c. . \], where \(a^{\dagger}_{\vec{R}_{i}},b^{\dagger}_{\vec{R}_{i}},c^{\dagger}_{\vec{R}_{i}} \left(a_{\vec{R}_{i}},b_{\vec{R}_{i}},c_{\vec{R}_{i}}\right)\) are creation (anihilation) operators of electrons in appropriate kind of atom on the lattice cell of the \(\vec{R}_{i}\) position.
Then going to the momentum space we get the diagonal form of the Hamiltonian with the following form,
\[ H=H_{NN}+H_{NNN}= \sum_{\vec{k}} \begin{pmatrix} a^{\dagger}_{\vec{k}} & b^{\dagger}_{\vec{k}} & c^{\dagger}_{\vec{k}} \end{pmatrix} \begin{pmatrix} 0 & 2t\cos{(\vec{k}\cdot\vec{a}_{1})} & 2t\cos{(\vec{k}\cdot\vec{a}_{2})} \cr 2t\cos{(\vec{k}\cdot \vec{a}_{1})}&0&2\tau \left(e^{i\phi}\cos{(\vec{k}\cdot (\vec{a}_1-\vec{a}_2))}+e^{-i\phi}\cos{(\vec{k}\cdot (\vec{a}_1+\vec{a}_2))} \right) \cr 2t\cos{(\vec{k}\cdot\vec{a}_2)}&2\tau \left( e^{i\phi}\cos{(\vec{k}\cdot (\vec{a}_1+\vec{a}_2))}+e^{-i\phi}\cos{(\vec{k}\cdot (\vec{a}_1-\vec{a}_2))} \right) &0 \end{pmatrix} \begin{pmatrix} a_{\vec{k}} \cr b_{\vec{k}} \\ c_{\vec{k}} \end{pmatrix} \]
fsyst, lead, lat = make_system(L=10, lead=True)
kwant.plot(fsyst)
# dictionary containing the parameters
# Lead bands: calculation with a better control
# sparse matrix diagonlization
# prepare H_0 and V for our lead
ham0 = fsyst.cell_hamiltonian(sparse=True)
_hop = fsyst.inter_cell_hopping(sparse=True)
shp = (_hop.shape[0], _hop.shape[0] - _hop.shape[1])
_zeros = sp.coo_matrix(shp, dtype=complex)
vhop = sp.hstack([_hop, _zeros])
momenta = np.linspace(-np.pi, np.pi, 301)
ens = []
for kpar in momenta:
# H_k = H_0 + V e^-ik + V^\dagger e^ik
hmat = vhop * np.exp(-1j * (kpar))
hmat += hmat.conjugate().transpose() + ham0
# evals = la.eigh( hmat, eigvals_only=True ) ## dense solver
evals = lsp.eigsh(
hmat, k=20, return_eigenvectors=False, which="LM", sigma=0.01, tol=10 ** (-8)
)
ens.append(np.sort(evals))
plt.grid()
plt.ylim(-0.01, 0.2)
plt.xlabel("momentum [1/a]")
plt.ylabel("energy")
plt.plot(momenta, ens)
plt.show()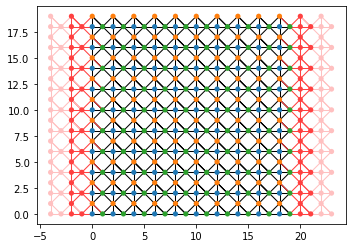
--------------------------------------------------------------------------- AttributeError Traceback (most recent call last) <ipython-input-45-d95fdb77c0c9> in <module>() 9 10 # prepare H_0 and V for our lead ---> 11 ham0 = fsyst.cell_hamiltonian(sparse=True) #.tocsc() 12 13 _hop = fsyst.inter_cell_hopping(sparse=True) AttributeError: 'FiniteSystem' object has no attribute 'cell_hamiltonian'
sys, left_lead = make_system()
kwant.plot(sys)
for t_2 in np.linspace(0.05, 1, 10):
sys, left_lead = make_system(
t_1=1,
t_2=t_2 * 0.5j,
)
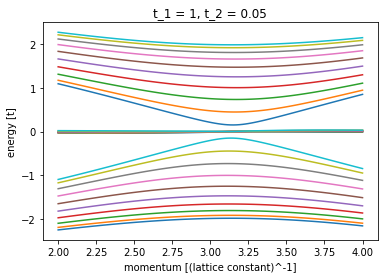
plot_bandstructure(
left_lead, np.linspace(2, 4, 100), t_2, title=f"t_1 = 1, t_2 = {t_2}"
)
plot_density(sys, 1, title=f"t_1 = 1, t_2 = {t_2}")
plt.show()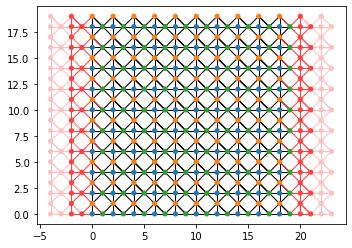
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-12-1192e6aa8cab> in <module>() 10 plot_bandstructure(left_lead, np.linspace(2,4, 100), t_2, title=f"t_1 = 1, t_2 = {t_2}") 11 #plot_conductance(sys, np.linspace(0,2,1000)) ---> 12 plot_density(sys, 1,title=f"t_1 = 1, t_2 = {t_2}") 13 #kwant.plotter.bands(left_lead) 14 <ipython-input-10-2bdac851c88a> in plot_density(sys, ener, it, title) 110 title2=title+".pdf" 111 --> 112 kwant.plotter.map(sys,psi,method='linear',vmin=0,title=f"t_1 = 1, t_2 = {t_2}") 113 114 J_0 = kwant.operator.Current(sys) TypeError: map() got an unexpected keyword argument 'title'